Phase-amplitude coupling: hidden in noise

March 06, 2016

See IPython Notebook accompanying this brief post.

In my admittedly short experience analyzing neural data, I have learned to appreciate a general principle: whatever signal I am looking for, it is probably masked in a lot of noise within the raw data. This is undoubtedly true for many cases of data analysis. Here, I’m going to show a specific example of this related to my research.

Our lab studies oscillations in neural recordings, and one oscillatory phenomena that has been identified across the brain is phase-amplitude coupling  (PAC). Briefly, PAC is a statistical correlation between the phase of one oscillation and the amplitude of an oscillation of higher frequency. The occurrence of PAC has been associated with improved multi-item working memory, learning, attention, decision making, with some evidence of a directional relationship of oscillations in one region driving oscillations downstream.

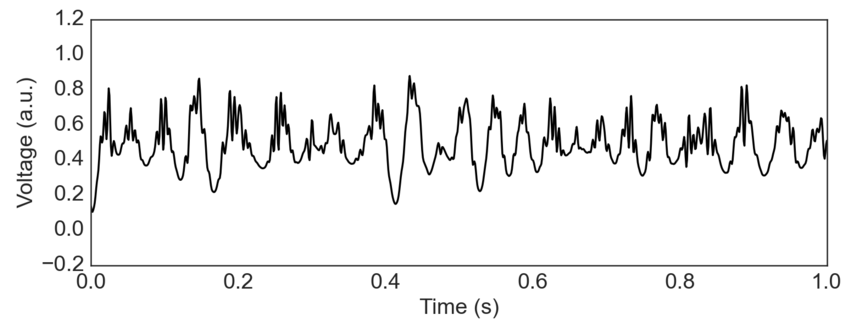
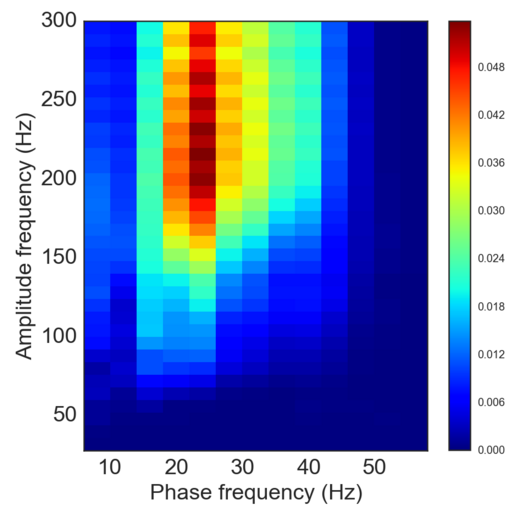
The simulated data above shows a high frequency oscillation that has increased amplitude at the peak of a lower frequency oscillation. Thus, it has high PAC. Together with Voytek lab post-doc, Erik Peterson, we wrote a python package for quantifying PAC. Using this package, we can visualize the coupling between these two oscillators with a comodulogram, below, which shows that the PAC is present between a 15-40Hz carrier oscillation and the amplitude of frequencies above 100Hz.

However, electrophysiological recordings will not have nearly as strong of a statistical dependence compared to our contrived example. In reality, one friend was searching for PAC in this voltage signal:

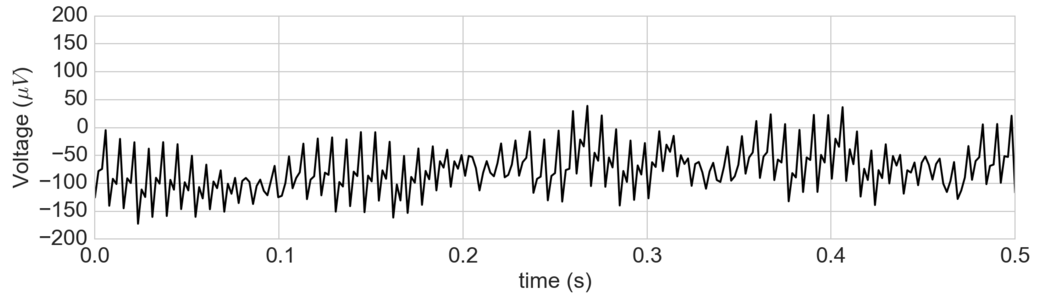
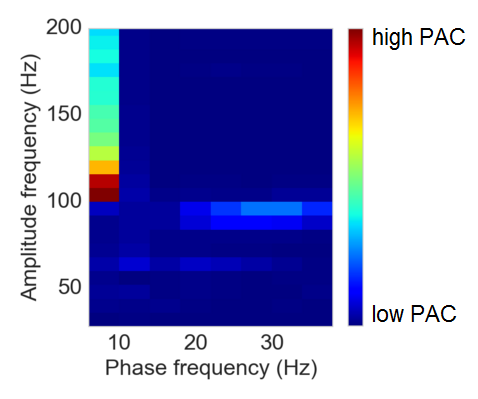
Given the clear artifacts in the time series, he was not detecting PAC in his comodulogram:

In this IPython Notebook, we show how to process this signal in order to extract the underlying PAC:

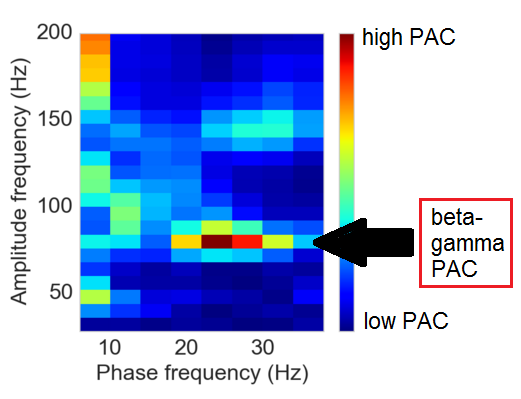
Later this year we will be publishing a paper with novel insight on PAC in the motor cortex of patients with Parkinson’s Disease. So stay tuned!