Formal proof that Farey Sequences yield Ford Circles
June 23, 2015
Another post inspired by Numberphile! In this episode, Francis Bonahon starts off by explaining Farey sequences, shown below up to N=8 (source). Each sequence is the ascending list of all simplified fractions between 0 and 1 with a maximum denominator of N.
What’s interesting about these? If you choose any number in a sequence, it is the result of Farey addition of the adjacent numbers in the sequence.
Here are a few examples to make it clear:
The fact that this holds for all consecutive fractions in this series is really cool, especially when you consider cases of large N. And there’s a proof here that shows:
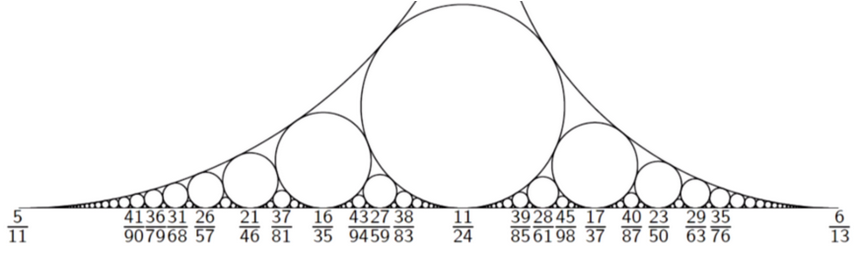
But what made this video much more interesting was when Bonahon introduced Ford circles. These circles, shown below (Numberphile), are constructed by drawing a circle with diameter 1/q2 immediately above each fraction p/q in a Farey sequence (in this case, N>100).
What’s cool about this? First, the circles are nonoverlapping. Second, we can choose any fraction and show that its circle is tangent to a circle on its left and right, and the numbers corresponding to these tangent circles yield the original number by Farey addition! Examples:
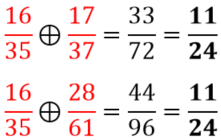
As Bonahon said in his video, “When we find something very surprising, we want to know: is this a coincidence? Or is there a deep fact behind that?” So, I wanted to prove this relationship between the Farey sequence and Ford circles to gain a deeper understanding of this fractal.
I started by noting that when two circles are tangent to one another, the line connecting the centers intersects the tangent point. Therefore, we can express this distance as the sum of the radii. A second way to express this distance is as the hypotenuse of a right triangle, as shown in the figure below. We have expressions for the legs of this triangle, and so can formulate an equation that must be satisfied in order for these circles to be tangent.

I then simplified the equation until I could do so no longer, and I saw something familiar.
The bottom line of this proof is identical to the requirement I stated above for two numbers to be adjacent in the Farey Sequence. Therefore, this proves that tangent circles in the Ford Circle fractal must represent Farey Neighbors. Yay!